Phương trình mũ cơ bản là một dạng toán quan trọng trong chương trình Toán học THPT, thường xuất hiện trong các kỳ thi và bài kiểm tra. Việc nắm vững phương pháp giải phương trình mũ giúp học sinh hiểu rõ hơn về hàm số mũ và ứng dụng trong thực tế. Chủ đề này bao gồm nhiều dạng bài tập khác nhau, từ phương trình đơn giản đến phương trình mũ chứa tham số. Để giải quyết các bài toán này, học sinh cần vận dụng linh hoạt các phương pháp như đưa về cùng cơ số, logarit hóa hoặc đặt ẩn phụ. Hãy cùng ôn tập qua các bài tập tiêu biểu trong chuyên đề này!
I. Lý thuyết phương trình mũ
\( a^x = b \) \((a > 0, a \neq 1)\).
– Phương trình có một nghiệm duy nhất khi và chỉ khi \( b > 0 \).
$ a^x = b \Leftrightarrow x = \log_a b \quad (a > 0, a \neq 1, b > 0) $
– Phương trình vô nghiệm khi và chỉ khi \( b \leq 0 \).
II. Bài tập vận dụng
Bài tập 1. Giải phương trình \( 3^{x-1} = 9 \).
Lời giải
$3^{x-1} = 9 \Leftrightarrow 3^{x-1} = 3^2 \Leftrightarrow x = 3.$
Bài tập 2. Giải phương trình \( 5^{x-1} = \left(\frac{1}{25}\right)^x \).
Lời giải
$5^{x-1} = \left(\frac{1}{25}\right)^x \Leftrightarrow 5^{x-1} = 5^{-2x} \Leftrightarrow x – 1 = -2x \Leftrightarrow x = \frac{1}{3}.$
Bài tập 3. Giải phương trình \( 3^{x^4 – 3x^2} = 81 \).
Lời giải
$3^{x^4 – 3x^2} = 81 \Leftrightarrow x^4 – 3x^2 = 4 \Leftrightarrow x^4 – 3x^2 – 4 = 0 $
$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {{x^2} = – 1}\\ {{x^2} = 4} \end{array}} \right.$
$ \Leftrightarrow {x^2} = 4 \Leftrightarrow x = \pm 2.$
Bài tập 4. Giải phương trình \( 7^{2x^2 + 5x + 4} = 49 \).
Lời giải
${7^{2{x^2} + 5x + 4}} = 49$ $ \Leftrightarrow {7^{2{x^2} + 5x + 4}} = {7^2}$
$ \Leftrightarrow 2{x^2} + 5x + 4 = 2$ $ \Leftrightarrow 2{x^2} + 5x + 2 = 0$
$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = – 2}\\ {x = – \frac{1}{2}} \end{array}} \right.$
Bài tập 5. Giải phương trình \( \left(\frac{3}{2}\right)^{x^2 – x – 5} = \left(\frac{2}{3}\right)^{2x+3} \).
Lời giải
Ta có
${\left( {\frac{3}{2}} \right)^{{x^2} – x – 5}} = {\left( {\frac{2}{3}} \right)^{2x + 3}}$ $ \Leftrightarrow {\left( {\frac{3}{2}} \right)^{{x^2} – x – 5}} = {\left( {\frac{3}{2}} \right)^{ – (2x + 3)}}$
$ \Leftrightarrow {x^2} – x – 5 = – 2x – 3$ $ \Leftrightarrow {x^2} + x – 2 = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = 1}\\ {x = – 2} \end{array}} \right.$
Bài tập 6. Giải phương trình \( 9^{\sin 2x} = 1 \).
Lời giải
Ta có $ 9^{\sin 2x} = 1 \Leftrightarrow \sin 2x = 0 \Leftrightarrow 2x = k2\pi \Leftrightarrow x = k\pi, (k \in \mathbb{Z}). $
Bài tập 7. Giải phương trình \( 2^{\sqrt{-x^2 + 2x + 4} – x + 4} = 4 \)
Lời giải
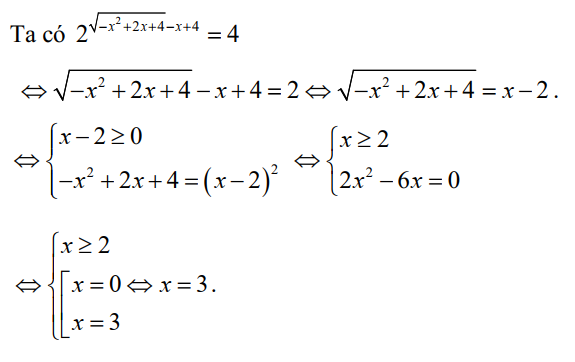
Vậy phương trình đã cho có nghiệm duy nhất là x = 3
Bài tập 8. Tìm \( m \) để phương trình \( 2020^{mx^2 – 2x + m – 2} = 1 \) có hai nghiệm trái dấu.
Lời giải
$2020^{mx^2 – 2x + m – 2} = 1 \Leftrightarrow mx^2 – 2x + m – 2 = 0.$
Phương trình đã cho có hai nghiệm trái dấu khi và chỉ khi \( m(m – 2) < 0 \Leftrightarrow 0 < m < 2 \).
Bài tập 9. Cho hàm số y = f(x) có bảng biến thiên như sau
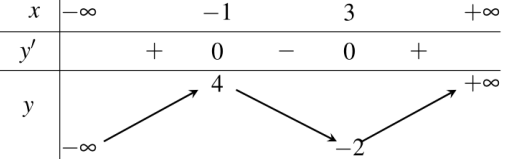
Tìm \( m \) phương trình \( 3^{2f(x) – m + 3} = 27 \) có 3 nghiệm phân biệt?
Lời giải
Ta có ${3^{2f(x) – m + 3}} = 27$ $ \Leftrightarrow 2f(x) = m$ $ \Leftrightarrow f(x) = \frac{m}{2}.$
Vậy phương trình đã cho có 3 nghiệm phân biệt khi
$ – 2 < \frac{m}{2} < 4$ $ \Leftrightarrow – 4 < m < 8.$
Bài tập 10. Cho hàm số \( y = x^3 – 3x + 2 \) có đồ thị như hình vẽ bên.
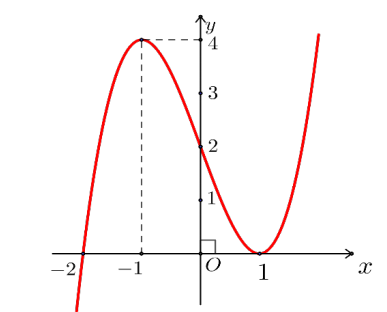
Tìm tất cả các giá trị thực của tham số \( m \) để phương trình ${4^{{x^3} – 3x – 1 – 2m}} = \frac{1}{{64}}$ có ba nghiệm thực phân biệt.
Lời giải
Ta có ${4^{{x^3} – 3x – 1 – 2m}} = \frac{1}{{64}}$ $ \Leftrightarrow {x^3} – 3x – 1 – 2m = – 3$ $ \Leftrightarrow {x^3} – 3x + 2 = 2m.$
Số nghiệm của phương trình \( x^3 – 3x + 2 – 2m = 0 \) là số giao điểm của đồ thị \( y = x^3 – 3x + 2 \) và đường thẳng \( y = 2m \).
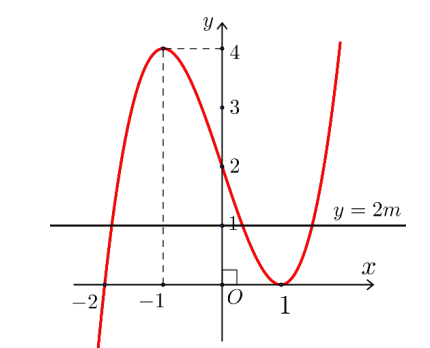
Nhìn vào đồ thị suy ra phương trình có 3 nghiệm phân biệt \( \Leftrightarrow 0 < 2m < 4 \Leftrightarrow 0 < m < 2 \).
Như vậy, phương trình mũ cơ bản là một phần quan trọng trong chương trình Toán học, giúp học sinh rèn luyện tư duy logic và khả năng biến đổi biểu thức. Bên cạnh đó, việc luyện tập thường xuyên với nhiều dạng bài tập khác nhau sẽ giúp bạn nắm vững kiến thức và áp dụng hiệu quả. Hy vọng qua chuyên đề này, bạn đã có thêm những kiến thức bổ ích và tự tin hơn khi đối mặt với các bài toán phương trình mũ cơ bản trong học tập và thi cử. Chúc bạn học tốt!