Phương trình logarit cơ bản là một dạng toán quan trọng trong chương trình Toán lớp 12, thường xuất hiện trong đề thi tốt nghiệp THPT quốc gia. Dạng bài này yêu cầu học sinh nắm vững các công thức logarit, điều kiện xác định và phương pháp biến đổi để giải quyết bài toán hiệu quả. Việc luyện tập các bài tập phương trình logarit cơ bản giúp nâng cao kỹ năng tư duy, xử lý hàm số và đạt điểm cao trong kỳ thi. Trong bài viết này, chúng tôi sẽ hướng dẫn chi tiết cách giải từng dạng toán, giúp bạn làm chủ phương trình logarit cơ bản nhanh chóng.
1. Lý thuyết phương trình logarit cơ bản
\(\log_a x = b\) \((x > 0, a > 0, a \neq 1)\) luôn có nghiệm duy nhất
$x = a^b \quad \text{với mọi } b.$
2. Bài tập
Bài tập 1. Giải phương trình sau: \(\log_3 x = 4\).
Lời giải
Điều kiện: \(x > 0\)
Ta có: \(\log_3 x = 4 \Leftrightarrow x = 3^4 \Leftrightarrow x = 81.\)
Vậy nghiệm của phương trình là \(x = 81\).
Bài tập 2. Giải phương trình sau: \(\log_2 (2x – 2) = 3\).
Lời giải
Điều kiện: \(2x – 2 > 0 \Leftrightarrow x > 1\)
Ta có: ${\log _2}(2x – 2) = 3$ $ \Leftrightarrow 2x – 2 = 8$ $ \Leftrightarrow 2x = 10 \Leftrightarrow x = 5$
Vậy nghiệm của phương trình là \(x = 5\).
Bài tập 3. Giải phương trình sau: \(\log_4 (x^2 + 5x + 10) = 2\).
Lời giải
Vì \( x^2 + 5x + 10 = \left( x + \frac{5}{2} \right)^2 + \frac{15}{4} > 0, \forall x \in \mathbb{R} \) nên tập xác định \( D = \mathbb{R} \).
Ta có: ${\log _4}\left( {{x^2} + 5x + 10} \right) = 2$ $ \Leftrightarrow {x^2} + 5x + 10 = 16$ $ \Leftrightarrow {x^2} + 5x – 6 = 0 \Leftrightarrow \left[ {\begin{array}{{20}{l}} {x = 1}\\ {x = – 6} \end{array}} \right.$
Vậy nghiệm của phương trình là \( x = 1 \) hay \( x = -6 \).
Bài tập 4. Giải phương trình sau: \( \log \left( x – 1 \right)^2 = 2 \).
Lời giải
Điều kiện: \( \left( x – 1 \right)^2 > 0 \Leftrightarrow x \neq 1 \)
Ta có: $\log {\left( {x – 1} \right)^2} = 2$ $ \Leftrightarrow {\left( {x – 1} \right)^2} = 100$ $ \Leftrightarrow \left| {x – 1} \right| = 10$ $ \Leftrightarrow \left[ {\begin{array}{{20}{l}} {x – 1 = 10}\\ {x – 1 = – 10} \end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{{20}{l}} {x = 11}\\ {x = – 9\left( {nhan} \right)} \end{array}} \right.$
Vậy nghiệm của phương trình là \( x = 11 \) hay \( x = -9 \).
Bài tập 5. Giải phương trình sau: $\log_5 \sqrt{x^2 – 3x + 1} = 1.$
Lời giải
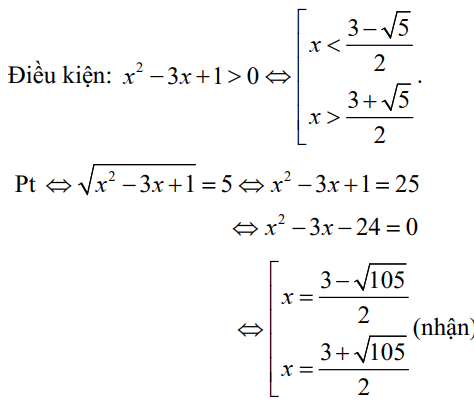
Vậy nghiệm của phương trình là $x = \frac{{3 – \sqrt {105} }}{2}$ hay $x = \frac{{3 + \sqrt {105} }}{2}$
Bài tập 6. Giải phương trình sau: ${\log _2}\left( {\sqrt {{x^2} – x + 1} + \sqrt {x + 1} } \right) = {\log _2}(x + 2).$
Lời giải
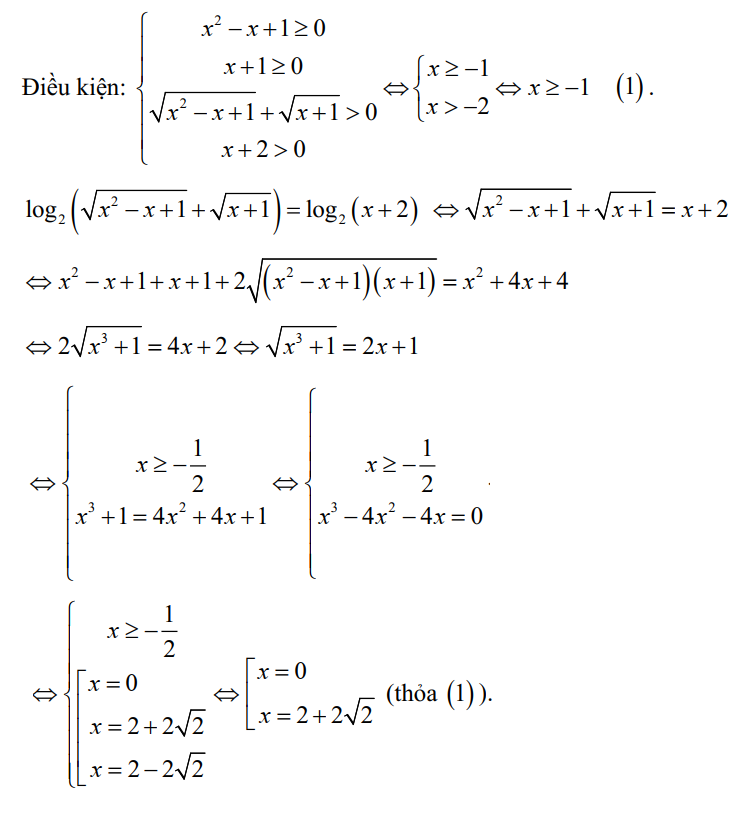
Vậy nghiệm của phương trình là \( x = 0 \) hay \( x = 2 + 2\sqrt{2} \).
Bài tập 7. Giải phương trình sau: \( \log (|\sin x|) = 0 \).
Lời giải
TXĐ: $D = R\backslash \{ k\pi \mid k \in Z\} $
Ta có: $\log (\left| {\sin x} \right|) = 0$ $ \Leftrightarrow \left| {\sin x} \right| = 1$ $ \Leftrightarrow \left[ {\begin{array}{{20}{l}} {\sin x = 1}\\ {\sin x = – 1} \end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{{20}{l}} {x = \frac{\pi }{2} + k2\pi ,\,\,k \in Z}\\ {x = – \frac{\pi }{2} + k2\pi ,\,\,k \in Z} \end{array}} \right.$
Vậy nghiệm của phương trình là $\left[ {\begin{array}{{20}{l}} {x = \frac{\pi }{2} + k2\pi ,\,\,k \in Z}\\ {x = – \frac{\pi }{2} + k2\pi ,\,\,k \in Z} \end{array}} \right.$
Bài tập 8. Giải phương trình sau: $ \log_2 (x – 5) + \log_2 (x + 2) = 3. $
Lời giải
Điều kiện: $ \begin{cases} x – 5 > 0 \\ x + 2 > 0 \end{cases} \Leftrightarrow \begin{cases} x > 5 \end{cases} $
Ta có: ${\log _2}(x – 5) + {\log _2}(x + 2) = 3$ $ \Leftrightarrow {\log _2}[(x – 5)(x + 2)] = 3$
$ \Leftrightarrow (x – 5)(x + 2) = 8$ $ \Leftrightarrow {x^2} – 3x – 18 = 0$ $ \Leftrightarrow \left[ {\begin{array}{{20}{l}} {x = – 3}\\ {x = 6} \end{array}} \right.$
Vậy nghiệm của phương trình là \( x = 6 \) (loại \( x = -3 \) do không thỏa mãn điều kiện).
Phương trình logarit cơ bản là một trong những dạng toán quan trọng, thường xuyên xuất hiện trong các kỳ thi, đặc biệt là đề thi tốt nghiệp THPT quốc gia. Để giải tốt dạng bài này, học sinh cần nắm vững lý thuyết logarit, điều kiện xác định, cũng như các phương pháp biến đổi phổ biến. Việc luyện tập thường xuyên với các bài tập từ cơ bản đến nâng cao sẽ giúp bạn thành thạo kỹ năng giải toán và tăng tốc độ làm bài. Hy vọng với những hướng dẫn và bài tập đã chia sẻ, bạn sẽ tự tin hơn khi đối mặt với phương trình logarit cơ bản trong kỳ thi. Hãy tiếp tục rèn luyện để đạt điểm cao và chinh phục mọi bài toán logarit!