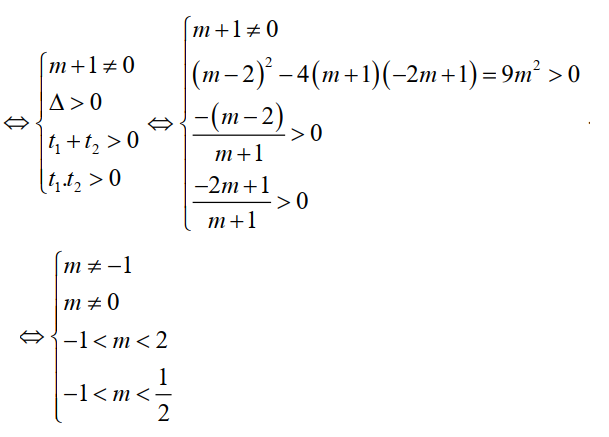Bài tập 1. Tìm tất cả giá trị thực của tham số \( m \) để phương trình \( 9^x – m.3^x + 6 = 0 \) có hai nghiệm phân biệt?
Lời giải
Đặt \( t = 3^x \) (\( t > 0 \)) thì phương trình trở thành \( t^2 – mt + 6 = 0 \) (1).
Phương trình đã cho có 2 nghiệm phân biệt khi và chỉ khi (1) có 2 nghiệm dương \( t_1, t_2 \) phân biệt
$ \Leftrightarrow \left\{ {\begin{array}{{20}{l}} {\Delta > 0}\\ {{t_1} + {t_2} > 0}\\ {{t_1}{t_2} > 0} \end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{{20}{l}} {{m^2} – 24 > 0}\\ {m > 0}\\ {6 > 0} \end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{{20}{l}} {|m| > 2\sqrt 6 }\\ {m > 0} \end{array}} \right.$ $ \Leftrightarrow m > 2\sqrt 6 .$
Bài tập 2. Tìm tất cả các giá trị nguyên của \( m \) để phương trình \( (m+1).16^x – 2(2m-3).4^x + 6m + 5 = 0 \) có 2 nghiệm trái dấu.
Lời giải
Đặt \( t = 4^x \), \( t > 0 \), khi đó phương trình trở thành:
$(m+1)t^2 – 2(2m-3)t + 6m + 5 = 0. \quad ()$
Để phương trình đã cho có hai nghiệm trái dấu thì phương trình \( () \) có hai nghiệm \( t_1, t_2 \) thỏa…
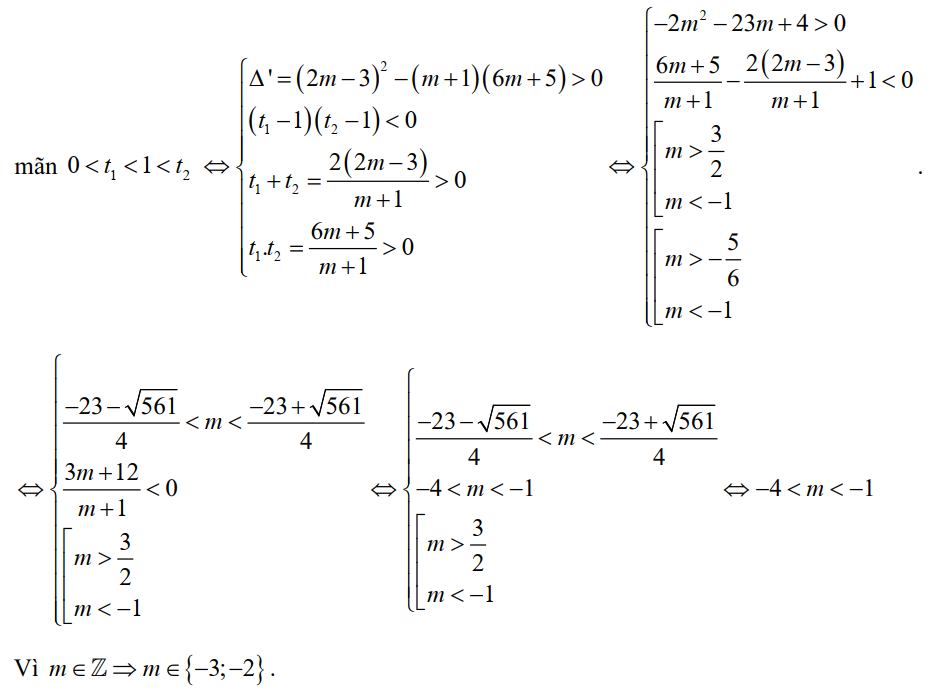
Bài tập 3. Tìm tất cả giá trị thực của tham số \( a \) để phương trình $(2+\sqrt{3})^x + (1-a)(2-\sqrt{3})^x – 4 = 0$ có 2 nghiệm phân biệt \( x_1, x_2 \) thỏa mãn \( x_1 – x_2 = \log_{2+\sqrt{3}} 3 \).
Lời giải
Phương trình:
$(2+\sqrt{3})^x + (1-a)(2-\sqrt{3})^x – 4 = 0 \quad (1)$
$\Leftrightarrow \left( \frac{2+\sqrt{3}}{2-\sqrt{3}} \right)^x + (1-a) \cdot \frac{-4}{(2-\sqrt{3})^x} = 0 \Leftrightarrow (2+\sqrt{3})^{2x} – 4 \cdot (2+\sqrt{3})^x + 1 – a = 0. $
Đặt \( (2+\sqrt{3})^x = t > 0 \), ta có phương trình $t^2 – 4t + 1 – a = 0. \quad (2)$

Bài tập 4. Tìm tất cả các giá trị thực của \( m \) để phương trình $4^x – 2.2^x + 2 = m$ có nghiệm \( x \in (-1;2) \).
Lời giải
Đặt \( t = 2^x \); vì \( x \in (-1;2) \) nên \( t \in \left( \frac{1}{2} ; 4 \right) \).
Khi đó phương trình trở thành $t^2 – 2t + 2 = m \quad ().$
Phương trình đã cho có nghiệm \( x \in (-1;2) \) khi và chỉ khi () có nghiệm \( t \in \left( \frac{1}{2} ; 4 \right) \).
Xét \( f(t) = t^2 – 2t + 2 \), với \( t \in \left[ \frac{1}{2} ; 4 \right] \).
Ta thấy \( f(t) \) liên tục trên \( t \in \left[ \frac{1}{2} ; 4 \right] \).
Có $f'(t) = 2t – 2; \quad f'(t) = 0 \Leftrightarrow t = 1.$
$\max\limits_{t \in \left[ \frac{1}{2} ; 4 \right]} f(t) = f(4) = 10; \quad \min\limits_{t \in \left[ \frac{1}{2} ; 4 \right]} f(t) = f(1) = 1.$
Từ đó suy ra () có nghiệm \( t \in \left( \frac{1}{2} ; 4 \right) \Rightarrow 1 \leq m < 10 \).
Bài tập 5. Tìm tất cả các giá trị thực của \( m \) để phương trình $\log_3^2 x + \log_3 x – 2m – 1 = 0$ có nghiệm.
Lời giải
Đặt \( t = \log_3 x \); \( t \in (0;1) \).
Phương trình trở thành: $t^2 + t – 2m – 1 = 0 \Leftrightarrow t^2 + t – 1 = 2m. \quad (1)$
Phương trình đã cho có nghiệm \( x \in (1;3) \) khi và chỉ khi (1) có nghiệm \( t \in (0;1) \).
Xét hàm số: $f(t) = t^2 + t – 1, \quad \text{với } t \in [0;1].$
Có: $f'(t) = 2t + 1 > 0, \quad \forall t \in (0;1) \Rightarrow f(t) \text{ đồng biến trên } (0;1).$
Phương trình (1) có nghiệm \( t \in (0;1) \)
$\Leftrightarrow f(0) < 2m < f(1) \Leftrightarrow -1 < 2m < 1 \Leftrightarrow m \in \left(-\frac{1}{2}; \frac{1}{2} \right).$
Vậy với \( m \in \left(-\frac{1}{2}; \frac{1}{2} \right) \), thì bài toán được thỏa mãn.
Bài tập 6. Tìm tất cả các giá trị thực của \( m \) để phương trình $(m+1) 25^{\log_2 x} + (m-2) x^{\log_2 5} – 2m + 1 = 0$ có hai nghiệm phân biệt \( x_1 \) và \( x_2 \) thỏa mãn \( x_1 x_2 = 4 \).
Lời giải
Điều kiện: \( x > 0 \).
Ta có: $(m+1) 25^{\log_2 x} + (m-2) x^{\log_2 5} – 2m + 1 = 0$
$\Leftrightarrow (m+1) 25^{\log_2 x} + (m-2) 5^{\log_2 x} – 2m + 1 = 0 \quad (1).$
Đặt \( t = 5^{\log_2 x} \) (\( t > 0 \)).
Khi đó phương trình (1) trở thành $ (m+1) t^2 + (m-2) t – 2m + 1 = 0 \quad (). $
Phương trình (*) có 2 nghiệm \( x_1 \) và \( x_2 \) phân biệt khi và chỉ khi phương trình () có 2 nghiệm \( t_1 \) và \( t_2 \).