Bạn đang tìm kiếm bài tập phương trình mũ nâng cao để rèn luyện tư duy toán học và chinh phục các kỳ thi quan trọng? Phương trình mũ là một phần không thể thiếu trong chương trình Toán THPT, đặc biệt xuất hiện nhiều trong đề thi học sinh giỏi và kỳ thi đại học. Để giải quyết các bài toán khó, bạn cần nắm chắc kiến thức nền tảng, thành thạo các phương pháp biến đổi và áp dụng linh hoạt các kỹ thuật giải nâng cao.
1. Phương pháp giải phương trình mũ
${a^{f(x)}} = {a^{g(x)}} \Leftrightarrow \left[ \begin{array}{l} a = 1\\ \left\{ \begin{array}{l} 0 < a \ne 1{\rm{ }}\\ {\rm{ }}f(x) = g(x) \end{array} \right. \end{array} \right.$
2. Bài tập phương trình mũ
Bài tập 1. Tính tổng các nghiệm của phương trình \( 2^{x^2 + 2x} = 8^{2 – x} \).
Lời giải
${2^{{x^2} + 2x}} = {8^{2 – x}}$ $ \Leftrightarrow {2^{{x^2} + 2x}} = {\left( {{2^3}} \right)^{2 – x}}$ $ \Leftrightarrow {2^{{x^2} + 2x}} = {2^{6 – 3x}}$ $ \Leftrightarrow {x^2} + 2x = 6 – 3x$ $ \Leftrightarrow {x^2} + 5x – 6 = 0$ $ \Leftrightarrow \left[ {\begin{array}{{20}{l}} {x = 1}\\ {x = – 6} \end{array}} \right.$
Vậy tổng các nghiệm của phương trình \( 2^{x^2 + 2x} = 8^{2 – x} \) bằng \( 1 + (-6) = -5 \).
Bài tập 2. Giải phương trình: \( 5^{x+1} – 5^x = 2^{x+1} + 2^{x+3} \).
Lời giải
${5^{x + 1}} – {5^x} = {2^{x + 1}} + {2^{x + 3}}$ $ \Leftrightarrow {5.5^x} – {5^x} = {2.2^x} + {2^3}{.2^x}$ $ \Leftrightarrow {4.5^x} = {10.2^x}$ $ \Leftrightarrow {\left( {\frac{5}{2}} \right)^x} = \frac{{10}}{4} = \frac{5}{2}$ $ \Leftrightarrow x = 1$
Vậy phương trình cho có nghiệm \( x = 1 \).
Bài tập 3. Giải phương trình: $\sqrt {{2^x} \cdot \sqrt[3]{{{4^x}.\sqrt[{3x}]{{0.125}}}}} = {4^3}\sqrt 2 .$
Lời giải
Điều kiện: $ \begin{cases} x \geq \frac{1}{3}, \\ 3x \in \mathbb{N}. \end{cases} $
Phương trình đã cho tương đương với phương trình:
$\sqrt {{2^x} \cdot {2^{\frac{x}{3}}} \cdot {{\left( {\frac{1}{8}} \right)}^{\frac{1}{{3x}}}}} = {2^2} \cdot {2^3}$ $ \Leftrightarrow {2^{\frac{x}{2} + \frac{x}{3} – \frac{1}{{2x}}}} = {2^3}$ $ \Leftrightarrow \frac{x}{2} + \frac{x}{3} – \frac{1}{{2x}} = \frac{7}{3}$ $ \Leftrightarrow 5{x^2} – 14x – 3 = 0$ $ \Leftrightarrow \left[ {\begin{array}{{20}{l}} {x = – \frac{1}{5}}\\ {x = 3} \end{array}} \right.$
Kết hợp với điều kiện, ta có \( x = 3 \) là nghiệm của phương trình.
Bài tập 4. Giải phương trình: $4^{x^2 – 3x + 2} + 4^{2x^2 + 6x + 5} = 4^{3x^2 + 3x + 7} + 1.$
Lời giải
Phương trình đã cho tương đương với phương trình:
${4^{{x^2} – 3x + 2}} + {4^{2{x^2} + 6x + 5}} = {4^{{x^2} – 3x + 2}} \cdot {4^{2{x^2} + 6x + 5}} + 1$ $ \Leftrightarrow {4^{{x^2} – 3x + 2}} – 1 + {4^{2{x^2} + 6x + 5}} – {4^{{x^2} – 3x + 2}} \cdot {4^{2{x^2} + 6x + 5}} = 0$ $ \Leftrightarrow \left( {{4^{{x^2} – 3x + 2}} – 1} \right)\left( {{4^{2{x^2} + 6x + 5}} – 1} \right) = 0$
Xét từng trường hợp:
– \( 4^{x^2 – 3x + 2} = 1 \Rightarrow x^2 – 3x + 2 = 0 \Rightarrow x = 1 \) hoặc \( x = 2 \).
– \( 4^{2x^2 + 6x + 5} = 1 \Rightarrow 2x^2 + 6x + 5 = 0 \), phương trình này vô nghiệm.
Vậy phương trình đã cho có 2 nghiệm: $\left[ {\begin{array}{{20}{l}} {x = 1}\\ {x = 2} \end{array}} \right.$
Bài tập 5. Tìm \( m \) để phương trình $5^{mx^2 + 2x + 3 + 2m} = 5^{m + x}$ có hai nghiệm trái dấu.
Lời giải
${5^{m{x^2} + 2x + 3 + 2m}} = {5^{m + x}}$ $ \Leftrightarrow m{x^2} + 2x + 3 + 2m = m + x$ $ \Leftrightarrow m{x^2} + x + 3 + m = 0\quad (2).$
Phương trình \((1)\) có 2 nghiệm trái dấu
\(\Leftrightarrow\) phương trình \((2)\) có 2 nghiệm trái dấu
\(\Leftrightarrow ac < 0\)
$\Leftrightarrow m(3 + m) < 0 \Leftrightarrow -3 < m < 0.$
Vậy \( m = \{-3; -2; -1\} \) thỏa mãn yêu cầu bài toán.
Bài tập 6. Tìm \( m \) để phương trình $ 7^{mx^2 + 2x} = 7^{2mx – m} $ có hai nghiệm \( x_1, x_2 \) thỏa mãn $ \frac{x_1^2}{x_2^2} + \frac{x_2^2}{x_1^2} \leq 2. $
Lời giải

Bài tập 7. Tìm \( m \) để phương trình: ${\left( {\frac{1}{5}} \right)^{\left| {{x^2} – 4x + 3} \right|}} = {m^4} – {m^2} + 1$ có 4 nghiệm phân biệt.
Lời giải
Phương trình cho tương đương với phương trình: $\left| x^2 – 4x + 3 \right| = \log_{\frac{1}{5}} (m^4 – m^2 + 1).$
Ta có bảng biến thiên của hàm số \( y = \left| x^2 – 4x + 3 \right| \).
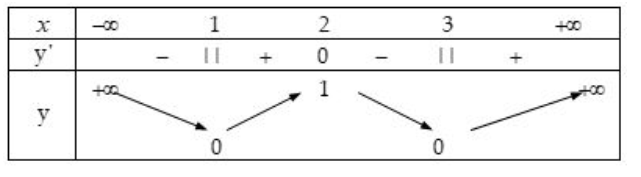
Dựa vào bảng biến thiên ta thấy phương trình có 4 nghiệm phân biệt khi và chỉ khi $0 < {\log _{\frac{1}{5}}}({m^4} – {m^2} + 1) < 1$ $ \Leftrightarrow \left\{ {\begin{array}{{20}{c}} {{m^4} – {m^2} < 0}\\ {5{m^4} – 5{m^2} + 4 > 0} \end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{{20}{c}} { – 1 < m < 1}\\ {m \ne 0} \end{array}} \right.$
Bài tập phương trình mũ nâng cao là một trong những dạng toán quan trọng giúp rèn luyện tư duy logic và kỹ năng giải toán hiệu quả. Để chinh phục những bài toán khó, bạn cần nắm vững lý thuyết, thành thạo các phương pháp giải và thường xuyên luyện tập với các dạng bài đa dạng. Hy vọng với những kiến thức và bài tập đã chia sẻ, bạn sẽ tự tin hơn khi đối mặt với các kỳ thi và nâng cao năng lực toán học của mình.
Hãy tiếp tục thực hành nhiều hơn nữa để làm chủ bài tập phương trình mũ nâng cao và đạt kết quả tốt nhất! Nếu bạn có bất kỳ câu hỏi hay cần tài liệu luyện tập, đừng ngần ngại để lại bình luận bên dưới nhé!