Bài tập phương trình logarit nâng cao là một trong những dạng toán quan trọng, thường xuất hiện trong các bài thi trên lớp, thi cuối kỳ và đặc biệt là kỳ thi tốt nghiệp THPT. Việc nắm vững phương pháp giải bài tập phương trình logarit nâng cao không chỉ giúp học sinh cải thiện tư duy toán học mà còn tăng cơ hội đạt điểm cao trong các kỳ thi quan trọng.
Trong bài viết này, chúng tôi sẽ hướng dẫn bạn cách tiếp cận và giải các bài tập phương trình logarit nâng cao, từ những dạng cơ bản đến các bài toán phức tạp đòi hỏi kỹ năng tư duy logic. Bên cạnh đó, chúng tôi cũng cung cấp hệ thống bài tập có lời giải chi tiết, giúp bạn luyện tập một cách hiệu quả nhất. Nếu bạn đang chuẩn bị cho các kỳ thi quan trọng như thi học kỳ, thi cuối cấp hay kỳ thi tốt nghiệp THPT, hãy cùng chúng tôi khám phá các phương pháp giải nhanh và chính xác nhất!
1. Phương pháp giải phương trình logarit
$ \log_a f(x) = \log_a g(x) \iff \begin{cases} 0 < a \neq 1 \\ f(x) = g(x) > 0 \end{cases} $
2. Bài tập phương trình logarit
Bài tập 1. Giải phương trình: $ \log_{25} (4x + 5)^2 + \log_5 x = \log_3 27. $
Lời giải
Điều kiện: \( x > 0 \).
Phương trình đã cho trở thành: $ \log_5 (4x + 5) + \log_5 x = 3 \iff 4x^2 + 5x – 125 = 0. $
Giải phương trình bậc hai: $\left[ {\begin{array}{{20}{l}} {x = 5}\\ {x = – \frac{{25}}{4}} \end{array}} \right.$
Vì \( x > 0 \), nên nghiệm của phương trình là \( x = 5 \).
Bài tập 2. Giải phương trình: $ \log_2 x + \log_3 x + \log_4 x = \log_{20} x $
Lời giải
Điều kiện: \( x > 0 \).
Phương trình đã cho tương đương với phương trình: $ \log_2 x + \frac{\log_2 x}{\log_2 3} + \frac{\log_2 x}{\log_2 4} = \frac{\log_2 x}{\log_2 20} $ $ \Leftrightarrow \log_2 x \left( 1 + \frac{1}{\log_2 3} + \frac{1}{\log_2 4} – \frac{1}{\log_2 20} \right) = 0 $ $ \Leftrightarrow \log_2 x = 0 \Leftrightarrow x = 1 $
Vậy phương trình đã cho có nghiệm \( x = 1 \).
Bài tập 3. Tìm tập nghiệm \( S \) của phương trình $ \log_3 (2x + 1) – \log_3 (x – 1) = 1. $
Lời giải
+ Ta có điều kiện xác định: $ \begin{cases} 2x + 1 > 0 \\ x – 1 > 0 \end{cases} \Leftrightarrow x > 1. $
+ Biến đổi phương trình: $ \log_3 (2x + 1) – \log_3 (x – 1) = 1 $ $ \Leftrightarrow \log_3 \left(\frac{2x+1}{x-1} \right) = 1 $ $ \Leftrightarrow \log_3 \left(\frac{2x+1}{x-1} \right) = \log_3 3 $ $ \Leftrightarrow \frac{2x+1}{x-1} = 3 $ $ \Leftrightarrow 2x+1 = 3(x-1) $ $ \Leftrightarrow 2x+1 – 3x + 3 = 0 $ $ \Leftrightarrow -x + 4 = 0 $ $ \Leftrightarrow x = 4. $
Vậy tập nghiệm của phương trình là \( S = \{4\} \).
Bài tập 4. Gọi \( x_1, x_2 \) là nghiệm của phương trình $ \log_x 2 – \log_{16} x = 0. $ Tính \( x_1 \cdot x_2 \).
Lời giải
Điều kiện: \( 0 < x \neq 1 \).
Ta có: $ \log_x 2 – \log_{16} x = 0 \Leftrightarrow \log_x 2 – \log_{2^4} x = 0. $ $ \Leftrightarrow \frac{1}{\log_2 x} – \frac{1}{4} \log_2 x = 0. $
Đặt \( t = \log_2 x \), phương trình trở thành: $ \frac{1}{t} – \frac{t}{4} = 0. $
Nhân cả hai vế với \( 4t \) (với \( t \neq 0 \)), ta được: $ 4 – t^2 = 0 \Leftrightarrow t^2 = 4. $ $\Leftrightarrow \left[ \begin{array}{l} {\log _2}x = 2 \Rightarrow x = 4\\ {\log _2}x = – 2 \Rightarrow x = \frac{1}{4} \end{array} \right.$
Vậy hai nghiệm của phương trình là \( x_1 = 4 \) và \( x_2 = \frac{1}{4} \).
Tích nghiệm: $ x_1 \cdot x_2 = 4 \cdot \frac{1}{4} = 1. $
Bài tập 5. Tổng tất cả các nghiệm thực của phương trình $ \log_2 x . \log_2 (32x) + 4 = 0 $ bằng bao nhiêu?
Lời giải
Điều kiện xác định: \( x > 0 \).
Phương trình đã cho: $ \log_2 x . \log_2 (32x) + 4 = 0 $ $ \Leftrightarrow \log_2 x . (\log_2 x + 5) + 4 = 0. $ $ \Leftrightarrow \log_2^2 x + 5 \log_2 x + 4 = 0. $
Giải phương trình bậc hai: $ \begin{cases} \log_2 x = -1 \Rightarrow x = \frac{1}{2}, \\ \log_2 x = -4 \Rightarrow x = \frac{1}{16}. \end{cases} $
Tổng tất cả các nghiệm của phương trình là: $ \frac{1}{2} + \frac{1}{16} = \frac{8}{16} + \frac{1}{16} = \frac{9}{16}. $
Do đó, tổng các nghiệm của phương trình đã cho bằng \( \frac{9}{16} \).
Bài tập 6. Ba số \( a + \log_2 3 \); \( a + \log_4 3 \); \( a + \log_8 3 \) theo thứ tự lập thành cấp số nhân. Công bội của cấp số nhân này bằng bao nhiêu?
Lời giải
Do các số \( a + \log_2 3 \); \( a + \log_4 3 \); \( a + \log_8 3 \) theo thứ tự là cấp số nhân nên: $ (a + \log_4 3)^2 = (a + \log_2 3)(a + \log_8 3) $ $ \Rightarrow a^2 + 2a \log_4 3 + \log_4^2 3 = a^2 + a \log_2 3 + a \log_8 3 + \log_2 3 . \log_8 3 $ $ \Rightarrow a \log_2 3 + \frac{1}{4} \log_2^2 3 = \frac{4}{3} a \log_2 3 + \frac{1}{3} \log_2^2 3 $ $ \Rightarrow \frac{1}{3} a = -\frac{1}{12} \log_2 3 \Rightarrow a = -\frac{1}{4} \log_2 3. $
Suy ra công bội của cấp số nhân là: $ \frac{-\frac{1}{4} \log_2 3 + \log_4 3}{\log_4 3 + \log_8 3} = \frac{\frac{1}{4} – \frac{1}{2}}{\frac{1}{2} – 1} = \frac{1}{3}. $
Bài tập 7. Cho phương trình \( \log_3^2 x – 2\log_{\sqrt{3}} x – 2\log_{\frac{1}{3}} x – 3 = 0 \) có hai nghiệm phân biệt là \( x_1, x_2 \). Tính giá trị của biểu thức \( P = \log_3 x_1 + \log_{27} x_2 \) biết \( x_1 < x_2 \).
Lời giải
Điều kiện: \( x > 0 \).
$ \log_3^2 x – 2\log_{\sqrt{3}} x – 2\log_{\frac{1}{3}} x – 3 = 0 $ $ \Leftrightarrow \log_3^2 x – 4\log_3 x + 2\log_3 x – 3 = 0 $ $ \Leftrightarrow \log_3^2 x – 2\log_3 x – 3 = 0 $ $ \Leftrightarrow \begin{cases} \log_3 x = -1 \\ \log_3 x = 3 \end{cases} $ $ \Leftrightarrow \begin{cases} x_1 = \frac{1}{3} \\ x_2 = 27 \end{cases} $
Vậy \( x_1 < x_2 \) nên \( x_1 = \frac{1}{3} \) và \( x_2 = 27 \).
$P = \log_3 x_1 + \log_{27} x_2 = \log_3 \frac{1}{3} + \log_{27} 27 = 0.$
Bài tập 8. Giải phương trình: $\log_2 \left( 8 – x^2 \right) + \log_{\frac{1}{2}} \left( \sqrt{1 + x} + \sqrt{1 – x} \right) – 2 = 0.$
Lời giải
Điều kiện: \( -1 \leq x \leq 1 \).
Phương trình đã cho tương đương với phương trình:
$ \log_2 \left( 8 – x^2 \right) = 2 + \log_2 \left( \sqrt{1 + x} + \sqrt{1 – x} \right) $ $ \Leftrightarrow 8 – x^2 = 4 \left( \sqrt{1 + x} + \sqrt{1 – x} \right) \quad () $
Đặt \( t = \sqrt{1 + x} + \sqrt{1 – x} \), phương trình () trở thành:
$ (t – 2)^2 (t^2 + 4t + 8) = 0 \Leftrightarrow t = 2. $ $ \sqrt{1 + x} + \sqrt{1 – x} = 2 \Leftrightarrow x = 0. $
Bài tập 9. Tìm \( m \) để phương trình:
$ \log_{\sqrt{2}} \left( mx – 6x^3 \right) + 2\log_{\frac{1}{2}} \left( -14x^2 + 29x – 2 \right) = 0 $ có 3 nghiệm phân biệt.
Lời giải
Phương trình đã cho tương đương với phương trình:
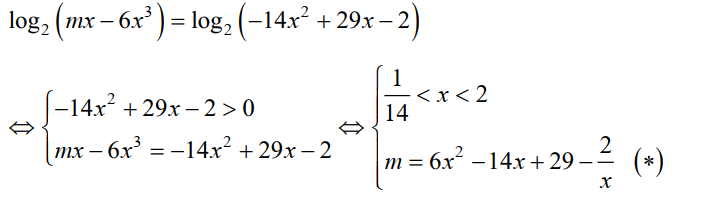
Phương trình đã cho có ba nghiệm phân biệt $ \Leftrightarrow (*) \text{ có hai nghiệm phân biệt } x \in \left( \frac{1}{14} ; 2 \right). $

Dựa vào bảng biến thiên, suy ra \((*)\) có ba nghiệm phân biệt \( x \in \left( \frac{1}{14} ; 2 \right) \) khi \( 19 < m < \frac{39}{2} \).
Kết luận
Việc chinh phục bài tập phương trình logarit nâng cao không chỉ giúp bạn nâng cao tư duy toán học mà còn là chìa khóa để đạt điểm cao trong các kỳ thi quan trọng như thi cuối kỳ, thi học sinh giỏi, thi tốt nghiệp THPT. Để làm tốt dạng bài này, bạn cần thường xuyên luyện tập, nắm vững phương pháp giải và rèn kỹ năng tư duy logic.
Hy vọng qua bài viết này, bạn đã có cái nhìn rõ hơn về cách tiếp cận và giải quyết bài tập phương trình logarit nâng cao một cách hiệu quả. Hãy tiếp tục thực hành, thử sức với nhiều dạng bài khác nhau và tự tin bước vào các kỳ thi! Nếu bạn cần thêm tài liệu hoặc hướng dẫn chi tiết, đừng quên theo dõi những bài viết tiếp theo để cập nhật kiến thức hữu ích nhất.
🚀 Bắt đầu luyện tập ngay hôm nay để làm chủ phương trình logarit và đạt điểm cao trong mọi kỳ thi!